机器学习中微积分基础
微积分是机器学习中的重要数学基础,机器学习中涉及到的很多公式都是微积分中的公式,因此微积分是机器学习中必须要掌握的数学基础。机器学习中的很多算法都是基于微积分的,例如:梯度下降算法,就是微积分中的导数运算,自变量和因变量都是函数,因此微积分对于学好、理解好机器学习,尤其是机器学习中涉及到的公式是非常重要的。
大学修了高等数学,有了微积分基础可以忽略下面的内容
导数
导数是微积分中的重要概念,假设函数y=f(x)在点x0的某个邻域内有定义,当自变量x在x0处有增量Δx时,相应的函数取得增量Δy=f(x0+Δx)−f(x0),如果Δy与Δx之比在Δx→0时的极限存在,那么就称y=f(x)在该点处可导,这个极限就是函数y=f(x)在点x0处的导数,记作f′(x0),即:f′(x0)=Δx→0limΔxΔy=Δx→0limΔxf(x0+Δx)−f(x0)。
切线
函数y=f(x)在点x0处的切线方程为:y=f(x0)+f′(x0)(x−x0)。
极值
函数y=f(x)在点x0处的极值,是指在x0的某个邻域内,当x=x0时,有f(x)<f(x0)或f(x)>f(x0),如果f(x)<f(x0),那么就称f(x0)是函数f(x)的极大值,如果f(x)>f(x0),那么就称f(x0)是函数y=f(x)的极小值。
对于可导函数y=f(x),如果在x0处有极值,那么f′(x0)=0。
最值
函数y=f(x)在区间[a,b]上的最大值和最小值,称为函数y=f(x)在区间[a,b]上的最值,记为:f(x)在[a,b]上的最大值为f(x)max,f(x)在[a,b]上的最小值为f(x)min。对于闭区间内的连续函数,最值一定存在,最值可能在区间的端点处取得,也可能在区间的内部取得(极值点)。
导数的表示
f(x)的导数表示为f′(x)=dxdy=dxdf(x)=dxdf(x)。
拉格朗日表示法(Lagrange′snotation)为:f′(x)
莱布尼茨表示法(Leibniz′snotation)为:dxdy=dxdf(x)
反函数及其导数
如果函数y=f(x)在区间Ix上是单调的、连续的、可导的,那么它的反函数y=f−1(x)在区间Iy上也是单调的、连续的、可导的,且有:[f−1(x)]′=f′(f−1(x))1。通俗一点的说法就是:反函数的导数等于原函数的导数的倒数。
假设f(x)的反函数为g(x),即f−1(x)=g(x)那么有:f(g(x))=x,g(f(x))=x,f′(g(x))g′(x)=1,g′(x)=f′(g(x))1。
简单一点的写法,函数y=f(x)经过反函数变换后,变成了x=f−1(y),那么有:f′(x)=dxdy,[f−1(y)]′=dydx,由这两个式子可以得到:[f−1(y)]′=f′(x)1。
导数的存在性
函数y=f(x)在点x0处可导的充分必要条件是:f(x)在点x0处的左、右导数存在且相等,即:f′(x0−)=f′(x0+)=f′(x0)。
函数的左导数:f′(x0−)=Δx→0−limΔxΔy=Δx→0−limΔxf(x0+Δx)−f(x0)。
函数的右导数:f′(x0+)=Δx→0+limΔxΔy=Δx→0+limΔxf(x0+Δx)−f(x0)。
导数的性质
- 导数的四则运算
- (C)′=0,其中C为常数。
- (Cf(x))′=Cf′(x),其中C为常数。
- (f(x)±g(x))′=f′(x)±g′(x)。
- (f(x)g(x))′=f′(x)g(x)+f(x)g′(x)。
- (g(x)f(x))′=[g(x)]2f′(x)g(x)−f(x)g′(x)。
- 导数的链式法则
- (f[g(x)])′=f′(g(x))g′(x)。dxdf[g(x)]=dgdfdxdg
- (f[g(h(x))])′=f′(g(h(x)))g′(h(x))h′(x)。dxdf[g(h(x))]=dgdfdhdgdxdh
切平面
函数z=f(x,y)在点(x0,y0)处的切平面方程为:z=f(x0,y0)+fx(x0,y0)(x−x0)+fy(x0,y0)(y−y0)。
偏导数
函数z=f(x,y)在点(x0,y0)处关于x的偏导数为:fx(x0,y0)=Δx→0limΔxf(x0+Δx,y0)−f(x0,y0)。
函数z=f(x,y)在点(x0,y0)处关于y的偏导数为:fy(x0,y0)=Δy→0limΔyf(x0,y0+Δy)−f(x0,y0)。
梯度
函数z=f(x,y)在点(x0,y0)处的梯度为:∇f(x0,y0)=(fx(x0,y0),fy(x0,y0))。
梯度与极值
函数z=f(x,y)在点(x0,y0)处可导,且∇f(x0,y0)=0,那么f(x,y)在点(x0,y0)处取得极值。
如果∇f(x0,y0)=0,那么f(x,y)在点(x0,y0)处取得极值,但是反过来不一定成立,即:∇f(x0,y0)=0,f(x,y)在点(x0,y0)处取得极值,但是f(x,y)在点(x0,y0)处取得极值,∇f(x0,y0)不一定等于0。
需要进行学习的内容,高数未讲的知识
优化
在机器学习中,导数的主要应用就是用于优化。优化是指在一定的约束条件下,使得目标函数达到最优值的过程。例如:在机器学习中,我们需要优化损失函数,使得损失函数达到最小值,这个过程就是优化过程。优化对于机器学习非常重要,因为在机器学习中,我们的目的就是找到最适合我们数据集的模型,而模型的好坏是由损失函数(误差)来衡量的。
平方损失优化
平方损失函数:L(w)=21i=1∑n(yi−wxi)2,其中w为模型参数,xi为样本特征,yi为样本标签,n为样本数量。
对数损失优化
对数损失函数:L(w)=i=1∑n(−yilog(yi^)−(1−yi)log(1−yi^)),其中w为模型参数,xi为样本特征,yi为样本标签,n为样本数量,yi^为模型预测值。
梯度优化
梯度优化是机器学习中常用的优化方法,梯度优化的思想是:根据梯度的信息,找到函数的最小值。
分析法
分析法是指直接求出梯度,然后令梯度为0,求出函数的极值点,然后通过分析函数的图像,找到函数的最小值。
分析法的缺点是:只能用于简单的函数,对于复杂的函数,很难求出函数的极值点。
梯度下降法
梯度下降法是机器学习中常用的优化方法,梯度下降法的思想是:根据梯度的信息,不断的更新优化,找到函数的最小值。
梯度下降法的步骤如下:
- 随机初始化参数w。
- 计算损失函数L(w)。
- 计算损失函数L(w)关于参数w的梯度∇L(w)。
- 更新参数w,w=w−α∇L(w),其中α为学习率。
- 重复步骤2-4,直到损失函数L(w)收敛。
- 返回参数w。
梯度下降法的缺点是:可能会陷入局部最优解。此时就需要使用随机梯度下降法,随机梯度下降法的思想是:每次更新参数时,随机选择一个样本,计算该样本的梯度,然后更新参数。
感知器/神经元
感知器(perceptron)的组成:

感知器由四部分组成:输入权重、加权求和、激活函数、输出。
感知器回归
感知器回归的思想是:根据输入的特征,预测输出的值。利用梯度下降更新参数,使得损失函数达到最小值。损失函数可以使用平方损失函数或者对数损失函数。
波士顿房价预测模型就是一个感知器回归模型。
感知器分类
感知器分类的思想是:根据输入的特征,预测输出的类别。利用梯度下降更新参数,使得损失函数达到最小值。损失函数可以使用平方损失函数或者对数损失函数。利用感知器得到的预测值不能很好的区分不同的类别,因此需要使用激活函数,比如使用sigmoid函数,将预测值转换为概率值,然后根据概率值判断类别。
鸢尾花分类模型就是一个感知器分类模型。
神经网络
神经网络(Neural Network)是机器学习中常用的模型,神经网络的思想是:根据输入的特征,预测输出的类别。利用梯度下降更新参数,使得损失函数达到最小值。神经网络就是多个感知器的组合,神经网络的每一层都是感知器,神经网络的每一层都是上一层的输出,神经网络的最后一层的输出就是预测值。

前向传播与反向传播
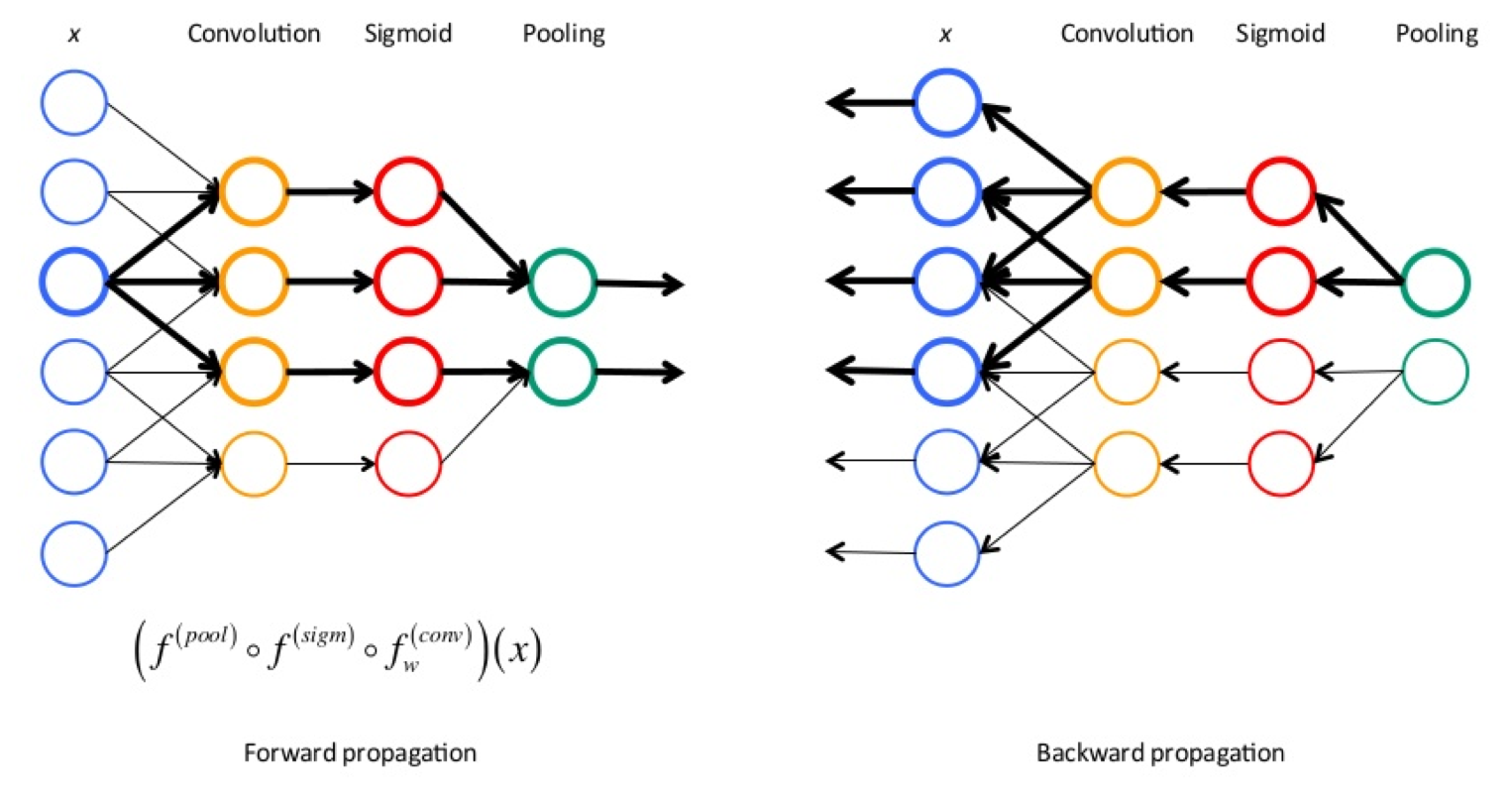
神经网络的训练过程中,前向传播和反向传播交替进行,前向传播通过训练数据和权重参数计算输出结果;反向传播通过导数链式法则计算损失函数对各参数的梯度,并根据梯度进行参数的更新。
前向传播是指从输入层开始,逐层向后计算,直到计算到输出层。
反向传播从输出层开始进行参数的更新,然后逐层向前更新参数,直到更新到输入层。
牛顿法
牛顿法其实就是用于求得函数的零点,即找到x0使得f(x0)=0。牛顿法的更新公式为xn+1=xn−f′(xn)f(xn)。
在机器学习中,我们需要求解损失函数的最小值,在最小值时,损失函数的导函数等于0,因此我们需要求得损失函数导数的零点,即找到x0使得f′(x0)=0,可以根据牛顿法找到该导数的零点。
海森矩阵
海森矩阵是一个方阵,它的每个元素是函数的二阶偏导数,海森矩阵的计算公式为:H(f(x))=⎣⎢⎢⎢⎢⎢⎢⎡∂x12∂2f(x)∂x2∂x1∂2f(x)⋮∂xn∂x1∂2f(x)∂x1∂x2∂2f(x)∂x22∂2f(x)⋮∂xn∂x2∂2f(x)⋯⋯⋱⋯∂x1∂xn∂2f(x)∂x2∂xn∂2f(x)⋮∂xn2∂2f(x)⎦⎥⎥⎥⎥⎥⎥⎤。
海森矩阵的逆矩阵为:H−1(f(x))=⎣⎢⎢⎢⎢⎢⎢⎡∂x12∂2f(x)∂x2∂x1∂2f(x)⋮∂xn∂x1∂2f(x)∂x1∂x2∂2f(x)∂x22∂2f(x)⋮∂xn∂x2∂2f(x)⋯⋯⋱⋯∂x1∂xn∂2f(x)∂x2∂xn∂2f(x)⋮∂xn2∂2f(x)⎦⎥⎥⎥⎥⎥⎥⎤−1。
海森矩阵与凹凸性
如果海森矩阵是正定矩阵,那么函数是凸函数,如果海森矩阵是负定矩阵,那么函数是凹函数。否则函数是的凹凸性不确定,可能会让我们陷入局部最优解。
多变量的牛顿法
多变量的牛顿法的更新公式为:xn+1=xn−H−1(f(xn))∇f(xn)。其中∇f(xn)为损失函数的梯度,H−1(f(xn))为损失函数的海森矩阵的逆矩阵,xn为参数组成的向量。





