线性代数

机器学习中线性代数基础

机器学习中的很多算法都是基于线性代数的，因此在学习机器学习的过程中，线性代数是必须要掌握的数学基础。机器学习神经网络中的卷积运算，就是线性代数中的矩阵运算，自变量和因变量都是矩阵形式，因此线性代数对于学好、理解好机器学习，尤其是机器学习中涉及到的公式是非常重要的。

大学修了线性代数，有了线性代数基础可以忽略下面的内容

方程组

方程组是线性代数中最基础的内容，例如小时候学习的鸡兔同笼问题就是一个最简单的方程组。方程组由方程组成，方程是由等号连接的两个代数式，代数式是由变量和常数构成的，变量是未知数，常数是已知数。例如：

$\begin{cases}{c} x+y+z&=6 \\ 2x-y+z&=3 \\ x+y-z&=0 \\ \end{cases}$

方程可能是直线，例如：$y=2x+1$，也可能是曲线，例如：$x^2+y^2=1$，也可能是平面，例如：$x+y+z=1$，也可能是空间曲面，例如：$x^2+y^2+z^2=1$。

线性方程组

线性方程组是由线性方程组成的方程组，线性方程是由变量的一次幂构成的方程，例如：

$\begin{cases}{c} x+y+z&=6 \\ 2x-y+z&=3 \\ x+y-z&=0 \\ \end{cases}$

就是一个线性方程组。
线性方程组可能有解，也可能无解，也可能有无穷多个解。结合矩阵的知识，可以辨认出线性方程组的解的情况。
线性方程组不一定每个式子都是唯一的，例如：a+b=1，2a+2b=2，这两个式子是等价的，因此线性方程组的解也是等价的，这两个式子只提供了一个信息。

奇异性

奇异性是线性方程组的一个重要概念，奇异性是指线性方程组的解的情况，奇异性分为三种情况：

1. 无解
2. 唯一解
3. 无穷多个解

行列式

行列式是线性代数中的一个重要概念，行列式是一个方阵，方阵是指行数和列数相等的矩阵，行列式的行数和列数都是n，那么行列式的阶数就是n。行列式的值是一个数字（可以通过计算得到），利用行列式可以很好的判断矩阵的奇异性。

奇异矩阵与非奇异矩阵

奇异矩阵是指行列式为0的矩阵，非奇异矩阵是指行列式不为0的矩阵。

线性相关与线性无关

线性相关是指线性方程组中的方程式之间存在线性关系，线性无关是指线性方程组中的方程式之间不存在线性关系。
线性相关

$k_1a_1+k_2a_2+...+k_na_n=0$

存在一组不全为0的k，使得上式成立。
线性无关

$k_1a_1+k_2a_2+...+k_na_n=0$

当且仅当k全为0时，上式成立。

解方程

利用方程组求解方程

矩阵行简化（高斯消元法）

在利用方程组求解的时候，我们往往会将其转化为矩阵进行求解，进行矩阵行化简的目的就是为了更好的求解。
矩阵的行简化可以将矩阵转化为行阶梯形矩阵或者行最简形矩阵。

行阶梯形矩阵

行阶梯形矩阵是指矩阵的每一行的非零元素都在每一行的零元素的左边，例如：

$\begin{pmatrix} 1 & 2 & 3 & 4 \\ 0 & 0 & 5 & 6 \\ 0 & 0 & 0 & 7 \\ \end{pmatrix}$

行最简形矩阵

行最简形矩阵是指矩阵的每一行的非零元素都在每一行的零元素的左边，且每一行的主元都是1，例如：

$\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{pmatrix}$

矩阵行简化的操作

一般来说，求解矩阵只需要化为行阶梯形矩阵就可以了。矩阵的行简化只能对行进行操作，不能对列进行操作，矩阵的行简化的操作有三种：

1. 交换两行
2. 用一个非零数乘以某一行
3. 用一个非零数乘以某一行，加到另一行上
   利用上面三种操作，可以将矩阵化为行阶梯形矩阵，矩阵的奇异性不会改变。

矩阵的秩

矩阵的秩是指矩阵的行阶梯形矩阵中非零行的行数，例如：

$\begin{pmatrix} 1 & 2 & 3 & 4 \\ 0 & 0 & 5 & 6 \\ 0 & 0 & 0 & 7 \\ \end{pmatrix}$

的秩是3。
矩阵的秩小于等于矩阵的行数和列数中的较小值。
利用矩阵的秩可以判断方程组的解的情况。

向量及其性质

向量是线性代数中的一个重要概念，向量是由一组有序的数构成的，例如：

$\begin{pmatrix} 1 \\ 2 \\ 3 \\ \end{pmatrix}$

向量的性质有：

1. 向量的加法
2. 向量的数乘
3. 向量的数量积（点积）
4. 向量的模
5. 向量的夹角
6. 向量的距离

向量的加法

向量的加法是指两个向量相加，例如：

$\begin{pmatrix} 1 \\ 2 \\ 3 \\ \end{pmatrix} + \begin{pmatrix} 4 \\ 5 \\ 6 \\ \end{pmatrix} = \begin{pmatrix} 5 \\ 7 \\ 9 \\ \end{pmatrix}$

向量的数乘

向量的数乘是指一个向量乘以一个数，例如：

$2 \begin{pmatrix} 1 \\ 2 \\ 3 \\ \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \\ 6 \\ \end{pmatrix}$

向量的数量积（点积）

向量的数量积是指两个向量相乘，例如：

$\begin{pmatrix} 1 \\ 2 \\ 3 \\ \end{pmatrix} \cdot （4 ，5 ，6） = 1 \times 4 + 2 \times 5 + 3 \times 6 = 32$

点积为0的两个向量是正交的。

向量的模

向量的模是指向量的长度，例如：

$\begin{pmatrix} 1 \\ 2 \\ 3 \\ \end{pmatrix}$

的模是：

$\sqrt{1^2+2^2+3^2}=\sqrt{14}$

向量的夹角

向量的夹角是指两个向量之间的夹角，例如：

$\begin{pmatrix} 1 \\ 2 \\ 3 \\ \end{pmatrix}$

和

$\begin{pmatrix} 4 \\ 5 \\ 6 \\ \end{pmatrix}$

的夹角是：

$\cos \theta = \frac{1 \times 4 + 2 \times 5 + 3 \times 6}{\sqrt{1^2+2^2+3^2} \times \sqrt{4^2+5^2+6^2}} = \frac{32}{\sqrt{14} \times \sqrt{77}}$

向量的距离

向量的距离是指两个向量之间的距离，例如：

$\begin{pmatrix} 1 \\ 2 \\ 3 \\ \end{pmatrix}$

和

$\begin{pmatrix} 4 \\ 5 \\ 6 \\ \end{pmatrix}$

的距离是：

$\sqrt{(1-4)^2+(2-5)^2+(3-6)^2}=\sqrt{27}$

矩阵与向量的乘法

矩阵与向量的乘法是指矩阵乘以向量，例如：

$\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{pmatrix} \begin{pmatrix} 1 \\ 2 \\ 3 \\ \end{pmatrix} = \begin{pmatrix} 14 \\ 32 \\ \end{pmatrix}$

矩阵为线性变换

矩阵可以看作是线性变换，例如：

$\begin{pmatrix} 3 & 2 \\ 4 & 5 \\ \end{pmatrix} \begin{pmatrix} 1 \\ 2 \\ \end{pmatrix} = \begin{pmatrix} 7 \\ 14 \\ \end{pmatrix}$

可以看作是：将向量（1，2）经过矩阵变换为向量（7，14）。

线性变换为矩阵

在上面的式子的基础上，矩阵的值为未知。即在不知道矩阵的具体值的情况下，可以通过多个式子的线性变换求出矩阵的值。

$\begin{pmatrix} ? & ? \\ ? & ? \\ \end{pmatrix} \begin{pmatrix} 0 \\ 1 \\ \end{pmatrix} = \begin{pmatrix} 2 \\ 3 \\ \end{pmatrix}$

$\begin{pmatrix} ? & ? \\ ? & ? \\ \end{pmatrix} \begin{pmatrix} 1 \\ 0 \\ \end{pmatrix} = \begin{pmatrix} 1 \\ 4 \\ \end{pmatrix}$

可以求出矩阵的值为：

$\begin{pmatrix} 1 & 2 \\ 4 & 3 \\ \end{pmatrix}$

矩阵的乘法

矩阵乘法需要满足左边矩阵的列数等于右边矩阵的行数。
用左边矩阵的行乘以右边矩阵的列，进行点积，得到的结果就是结果矩阵的元素。
即左边矩阵第a行与右边矩阵第b列进行点积，得到的数字就是结果矩阵第a行第b列的元素，例如：

$\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{pmatrix} \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ \end{pmatrix} = \begin{pmatrix} 22 & 28 \\ 49 & 64 \\ \end{pmatrix}$

矩阵的乘法不满足交换律，但是满足结合律。

单位矩阵

单位矩阵是指对角线上的元素为1，其余元素为0的矩阵，例如：

$\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$

单位矩阵与向量的乘法满足：

$\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} a \\ b \\ c \\ \end{pmatrix} = \begin{pmatrix} a \\ b \\ c \\ \end{pmatrix}$

单位矩阵与矩阵的乘法满足：

$\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{pmatrix} = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{pmatrix}$

逆矩阵

逆矩阵是指矩阵与其逆矩阵相乘得到单位矩阵，即$A*A^{-1}=E$，例如：

$\begin{pmatrix} 1 & 2 \\ 3 & 4 \\ \end{pmatrix} \begin{pmatrix} 1 & -2 \\ -3 & 1 \\ \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix}$

因此矩阵

$\begin{pmatrix} 1 & -2 \\ -3 & 1 \\ \end{pmatrix} 的逆矩阵为 \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ \end{pmatrix}$

$\begin{pmatrix} 1 & 2 \\ 3 & 4 \\ \end{pmatrix} 的逆矩阵为 \begin{pmatrix} 1 & -2 \\ -3 & 1 \\ \end{pmatrix}$

矩阵的逆矩阵不一定存在，只有非奇异矩阵才有逆矩阵。

行列式的乘法

行列式的乘法是指两个行列式相乘，例如：

$\begin{vmatrix} 1 & 2 \\ 3 & 4 \\ \end{vmatrix} \begin{vmatrix} 5 & 6 \\ 7 & 8 \\ \end{vmatrix} = \begin{vmatrix} 1 \times 5 + 2 \times 7 & 1 \times 6 + 2 \times 8 \\ 3 \times 5 + 4 \times 7 & 3 \times 6 + 4 \times 8 \\ \end{vmatrix} = \begin{vmatrix} 19 & 22 \\ 43 & 50 \\ \end{vmatrix}$

$det(A)*det(B) = det(AB)$
$det(A)*det(A^{-1}) = det(E)$
$det(A^{-1}) = \frac{1}{det(A)}$

线性代数的基

一系列向量$v_{1},v_{2}…v_{d}$具有两个特性，向量的个数足够但又不会太多，这是“基”的基本含义。因此空间的“基”是指一个向量组。而向量组里的这些向量具有两种性质：

1. 它们是线性无关的；
2. 它们生成整个空间；
3. n维空间$R^n$中的基的个数为n。
   例如：在三维空间$R^3$中，一组常见的基是：

$\begin{pmatrix} 1 \\ 0 \\ 0 \\ \end{pmatrix} \begin{pmatrix} 0 \\ 1 \\ 0 \\ \end{pmatrix} \begin{pmatrix} 0 \\ 0 \\ 1 \\ \end{pmatrix}$

用矩阵来描述，它们构成了一个单位阵。

特征值与特征向量

特征值与特征向量的关系是：

$A\vec{v}=\lambda\vec{v}$

其中A是一个矩阵，$\vec{v}$是一个向量（特征向量），$\lambda$是一个标量（特征值）。
矩阵$A$当然是一个变换，然后这个变换的特殊之处是当它作用在特征向量上的时候，只发生了缩放变换，它的方向并没有改变，并没有旋转。
获得了一个矩阵之后，可以通过行列式求出特征值，然后通过特征值结合矩阵求解得出特征向量。

正定矩阵

正定矩阵是指矩阵的特征值都大于0的矩阵，例如：

$\begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix}$

的特征值为1，因此是正定矩阵。
正定矩阵的公式为：

$f(A) = x^TAx>0$

其中x是任意一个非零向量，A是正定矩阵。

正交矩阵

正交矩阵是指矩阵的行向量两两正交，且行向量的模为1，例如：

$\begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \end{pmatrix}$

的行向量两两正交，且行向量的模为1，因此是正交矩阵。

额外了解

标量对向量求导

$\frac{\partial f}{\partial \vec{v}}$

$\vec{v} = (v_1, v_2, v_3)$

标量对向量求导是指标量对向量中的每个元素求导，例如：

$\frac{\partial f}{\partial \vec{v}}= \begin{pmatrix} \frac{\partial f}{\partial v_1} \\ \frac{\partial f}{\partial v_2} \\ \frac{\partial f}{\partial v_3} \\ \end{pmatrix}$

$\vec{v}$原本为行向量，求导后$\frac{\partial f}{\partial \vec{v}}$变为列向量。

向量对标量求导

$\frac{\partial \vec{v}}{\partial x}$

$\vec{v} = \begin{pmatrix} v_1 \\ v_2 \\ v_3\\ \end{pmatrix}$

向量对标量求导的结果是一个向量，向量的每个元素都是对应元素的求导结果，例如：

$\frac{\partial \vec{v}}{\partial x}= \begin{pmatrix} \frac{\partial v_1}{\partial x} \\ \frac{\partial v_2}{\partial x} \\ \frac{\partial v_3}{\partial x} \\ \end{pmatrix}$

$\vec{v}$是一个列向量，求导后$\frac{\partial \vec{v}}{\partial x}$还是列向量。

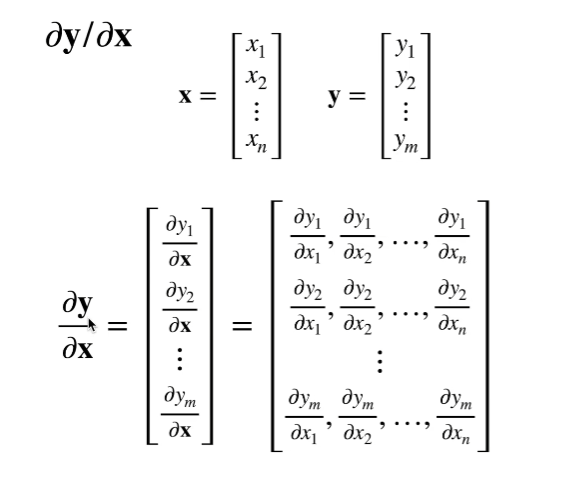
向量对向量求导

$\frac{\partial \vec{v}}{\partial \vec{w}}$

$\vec{v} = \begin{pmatrix} v_1 \\ v_2 \\ v_3\\ \end{pmatrix}$

$\vec{w} = \begin{pmatrix} w_1 \\ w_2 \\ w_3\\ \end{pmatrix}$

向量对向量求导的结果是一个矩阵，矩阵的每个元素都是对应元素的求导结果，例如：

$\frac{\partial \vec{v}}{\partial \vec{w}}= \begin{pmatrix} \frac{\partial v_1}{\partial w_1} & \frac{\partial v_1}{\partial w_2} & \frac{\partial v_1}{\partial w_3} \\ \frac{\partial v_2}{\partial w_1} & \frac{\partial v_2}{\partial w_2} & \frac{\partial v_2}{\partial w_3} \\ \frac{\partial v_3}{\partial w_1} & \frac{\partial v_3}{\partial w_2} & \frac{\partial v_3}{\partial w_3} \\ \end{pmatrix}$

$\vec{v}$和$\vec{w}$都是列向量，求导后$\frac{\partial \vec{v}}{\partial \vec{w}}$是一个矩阵。

矩阵对标量求导

$\frac{\partial A}{\partial x}$

矩阵对标量求导的结果是一个矩阵，矩阵的每个元素都是对应元素的求导结果，例如：

$\frac{\partial A}{\partial x}= \begin{pmatrix} \frac{\partial a_{11}}{\partial x} & \frac{\partial a_{12}}{\partial x} \\ \frac{\partial a_{21}}{\partial x} & \frac{\partial a_{22}}{\partial x} \\ \end{pmatrix}$

标量、向量、矩阵求导的关系

链式求导