概率与统计

机器学习中概率与统计基础

概率与统计是机器学习中的重要数学基础，机器学习中涉及到的很多公式都是概率与统计中的公式，因此概率与统计是机器学习中必须要掌握的数学基础。机器学习中的很多算法都是基于概率与统计的，例如：朴素贝叶斯算法，就是概率与统计中的贝叶斯公式，自变量和因变量都是随机变量，因此概率与统计对于学好、理解好机器学习，尤其是机器学习中涉及到的公式是非常重要的。

大学修了概率论与数理统计，有了概率与统计基础可以忽略下面的内容

概率学

概率

概率是随机事件发生的可能性，概率的取值范围是[0,1]，概率越大，随机事件发生的可能性越大，概率越小，随机事件发生的可能性越小。概率的计算公式如下：

$P(A)=\frac{m}{n}$

其中，$P(A)$表示事件A发生的概率，$m$表示事件A发生的次数，$n$表示事件A发生的总次数。

概率的补集

概率的补集是指事件A不发生的概率，概率的补集的计算公式如下：

$P(\bar{A})=1-P(A)$

其中，$P(\bar{A})$表示事件A不发生的概率，$P(A)$表示事件A发生的概率。

不相容事件的概率和

不相容事件是指两个事件不能同时发生的事件，不相容事件的概率和的计算公式如下：

$P(A\cup B)=P(A)+P(B)$

其中，$P(A\cup B)$表示事件A和事件B发生的概率和，$P(A)$表示事件A发生的概率，$P(B)$表示事件B发生的概率。

相容事件的概率和

相容事件是指两个事件可以同时发生的事件，相容事件的概率和的计算公式如下：

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

其中，$P(A\cup B)$表示事件A和事件B发生的概率和，$P(A)$表示事件A发生的概率，$P(B)$表示事件B发生的概率，$P(A\cap B)$表示事件A和事件B发生的概率积。

独立性

独立性是指两个事件相互独立，一个事件的发生不会影响另一个事件的发生，独立性的计算公式如下：

$P(A|B)=P(A)$

其中，$P(A|B)$表示事件A在事件B发生的条件下发生的概率，$P(A)$表示事件A发生的概率。

条件概率

条件概率是指事件A在事件B发生的条件下发生的概率，条件概率的计算公式如下：

$P(A|B)=\frac{P(A\cap B)}{P(B)}$

其中，$P(A|B)$表示事件A在事件B发生的条件下发生的概率，$P(A\cap B)$表示事件A和事件B发生的概率积，$P(B)$表示事件B发生的概率。

独立事件的概率积

独立事件是指两个事件相互独立，一个事件的发生不会影响另一个事件的发生，独立事件的概率积的计算公式如下：

$P(A\cap B)=P(A)\cdot P(B)$

其中，$P(A\cap B)$表示事件A和事件B发生的概率积，$P(A)$表示事件A发生的概率，$P(B)$表示事件B发生的概率。

贝叶斯公式

贝叶斯公式是指事件A在事件B发生的条件下发生的概率，贝叶斯公式的计算公式如下：

$P(A|B)=\frac{P(B|A)\cdot P(A)}{P(B)}$

其中，$P(A|B)$表示事件A在事件B发生的条件下发生的概率，$P(B|A)$表示事件B在事件A发生的条件下发生的概率，$P(A)$表示事件A发生的概率，$P(B)$表示事件B发生的概率。

先验与后验

先验概率是指在没有任何先验知识的情况下，事件A发生的概率，先验概率的计算公式如下：

$P(A)=\frac{m}{n}$

其中，$P(A)$表示事件A发生的概率，$m$表示事件A发生的次数，$n$表示事件A发生的总次数。
后验概率是指在有了先验知识的情况下，事件A发生的概率，后验概率的计算公式如下：

$P(A|B)=\frac{P(B|A)\cdot P(A)}{P(B)}$

其中，$P(A|B)$表示事件A在事件B发生的条件下发生的概率，$P(B|A)$表示事件B在事件A发生的条件下发生的概率，$P(A)$表示事件A发生的概率，$P(B)$表示事件B发生的概率。

全概率公式

全概率公式是指事件A发生的概率，全概率公式的计算公式如下：

$P(A)=\sum_{i=1}^{n}P(A|B_i)\cdot P(B_i)$

其中，$P(A)$表示事件A发生的概率，$P(A|B_i)$表示事件A在事件$B_i$发生的条件下发生的概率，$P(B_i)$表示事件$B_i$发生的概率。

随机变量

随机变量是指随机试验结果的数值表示，随机变量的取值范围是实数集，随机变量的计算公式如下：

$X(\omega)=x$

其中，$X(\omega)$表示随机变量，$\omega$表示随机试验的结果，$x$表示随机变量的取值。

离散型随机变量

离散型随机变量是指随机变量的取值是有限个或者可数个的随机变量，离散型随机变量的计算公式如下：

$P(X=x_i)=p_i$

其中，$P(X=x_i)$表示随机变量取值为$x_i$的概率，$p_i$表示随机变量取值为$x_i$的概率。

二项分布

二项分布是指n次独立重复试验中，事件A发生k次的概率，二项分布的计算公式如下：

$P(X=k)=C_n^kp^k(1-p)^{n-k}$

其中，$P(X=k)$表示事件A发生k次的概率，$C_n^k$表示从n次独立重复试验中取出k次的组合数，$p^k$表示事件A发生k次的概率，$(1-p)^{n-k}$表示事件A不发生n-k次的概率。

泊松分布

泊松分布是指单位时间内随机事件发生的次数，泊松分布的计算公式如下：

$P(X=k)=\frac{\lambda^k}{k!}e^{-\lambda}$

其中，$P(X=k)$表示单位时间内随机事件发生k次的概率，$\lambda$表示单位时间内随机事件发生的平均次数，$k!$表示k的阶乘，$e$表示自然对数的底数。

连续型随机变量

连续型随机变量是指随机变量的取值是无限个的随机变量，对于连续型随机变量，在每一点x处的取值为：

$P(X=x)=0$

概率密度函数

概率密度函数是指连续型随机变量的概率函数，概率密度函数的计算公式如下：

$P(a\leq X\leq b)=\int_a^bf(x)dx$

其中，$P(a\leq X\leq b)$表示随机变量取值在a和b之间的概率，$f(x)$表示概率密度函数，$dx$表示微元。

分布函数

分布函数是指随机变量取值在某个数值之前的概率，分布函数的计算公式如下：

$F(x)=P(X\leq x)$

其中，$F(x)$表示随机变量取值在x之前的概率，$P(X\leq x)$表示随机变量取值在x之前的概率。

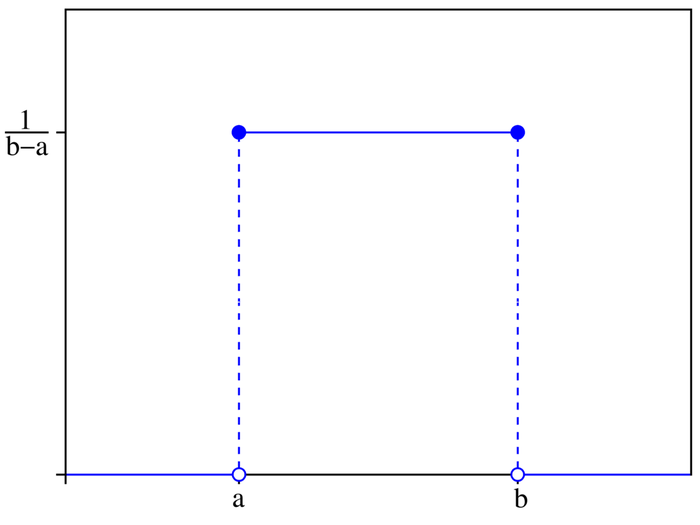
均匀分布

均匀分布是指随机变量在某个区间内的概率密度函数，均匀分布的计算公式如下：

$f(x)=\begin{cases} \frac{1}{b-a},&a\leq x\leq b\\ 0,&x<a或x>b \end{cases}$

其中，$f(x)$表示随机变量在某个区间内的概率密度函数，$a$表示随机变量的最小值，$b$表示随机变量的最大值。

正态分布

正态分布是指随机变量在某个区间内的概率密度函数，正态分布的计算公式如下：

$f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

其中，$f(x)$表示随机变量在某个区间内的概率密度函数，$\mu$表示随机变量的均值，$\sigma$表示随机变量的标准差。

卡方分布

卡方分布是由n个相互独立的标准正态随机变量的平方和构成的

$\chi^2(n)=\sum_{i=1}^nX_i^2$

$X_i$为标准正态随机变量，彼此相互独立。
卡方分布的计算公式如下：

$f(x)=\frac{1}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}$

其中，$f(x)$表示随机变量在某个区间内的概率密度函数，$\Gamma(\frac{n}{2})$表示伽马函数。

伽马函数

伽马函数的计算公式如下：

$\Gamma(\alpha)=\int_0^{+\infty}x^{\alpha-1}e^{-x}dx$

伽马函数的性质如下：

$\Gamma(\alpha+1)=\alpha\Gamma(\alpha)$

$\Gamma(1)=1$

$\Gamma(\frac{1}{2})=\sqrt{\pi}$

$\Gamma(n+1)=n!$

期望

期望是指随机变量的平均值，离散型随机变量的期望的计算公式如下：

$E(X)=\sum_{i=1}^nx_iP(X=x_i)$

其中，$E(X)$表示随机变量的期望，$x_i$表示随机变量的取值，$P(X=x_i)$表示随机变量取值为$x_i$的概率。
连续型随机变量的期望的计算公式如下：

$E(X)=\int_{-\infty}^{+\infty}xf(x)dx$

其中，$E(X)$表示随机变量的期望，$x$表示随机变量的取值，$f(x)$表示随机变量的概率密度函数。
期望的性质如下：

$E(a)=a$

$E(aX+b)=aE(X)+b$

$E(E(X))=E(X)$

$E(X+Y)=E(X)+E(Y)$

$E(XY)=E(X)E(Y)，当X，Y相互独立$

其中，$E(X)$表示随机变量的期望，$X$表示随机变量，$Y$表示随机变量。

方差

方差是指随机变量的离散程度，方差的计算公式如下：

$D(X)=E[(X-E(X))^2]=E(X^2)-[E(X)]^2$

对于离散型随机变量，方差的计算公式如下：

$D(X)=\sum_{i=1}^n(x_i-E(X))^2P(X=x_i)$

对于连续型随机变量，方差的计算公式如下：

$D(X)=\int_{-\infty}^{+\infty}(x-E(X))^2f(x)dx$

其中，$D(X)$表示随机变量的方差，$E(X^2)$表示随机变量的二阶矩，$[E(X)]^2$表示随机变量的一阶矩的平方。
方差的性质如下：

$D(a)=0$

$D(aX+b)=a^2D(X)$

$D(aX+bY)=a^2D(X)+b^2D(Y)+2abCov(X,Y),Cov(X,Y)为协方差$

$Cov(X,Y)=E[(X-E(X))(Y-E(Y))]$

$D(X+Y)=D(X)+D(Y)，当X，Y相互独立$

其中，$D(X)$表示随机变量的方差，$X$表示随机变量，$Y$表示随机变量。

协方差

协方差是指随机变量之间的相关程度，协方差的计算公式如下：

$Cov(X,Y)=E[(X-E(X))(Y-E(Y))]$

协方差的性质如下：

$Cov(X,Y)=Cov(Y,X)$

$Cov(X,X)=D(X)$

$Cov(aX,bY)=abCov(X,Y)$

$Cov(X+Y,Z)=Cov(X,Z)+Cov(Y,Z)$

$Cov(aX+bY,Z)=aCov(X,Z)+bCov(Y,Z)$

其中，$Cov(X,Y)$表示随机变量之间的协方差，$X$表示随机变量，$Y$表示随机变量，$Z$表示随机变量。

标准差

标准差是指随机变量的离散程度，标准差的计算公式如下：

$\sigma(X)=\sqrt{D(X)}$

其中，$\sigma(X)$表示随机变量的标准差，$D(X)$表示随机变量的方差。

标准正态分布

标准正态分布是指随机变量的均值为0，方差为1的正态分布，标准正态分布的计算公式如下：

$f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$

其中，$f(x)$表示随机变量的概率密度函数。
正态分布转化为标准正态分布的计算公式如下：

$Z=\frac{X-\mu}{\sigma}$

其中，$Z$表示标准正态分布，$X$表示正态分布，$\mu$表示正态分布的均值，$\sigma$表示正态分布的标准差。

矩

矩是指随机变量的期望，矩的计算公式如下：

$\mu_k=E(X^k)$

其中，$\mu_k$表示随机变量的k阶矩，$E(X^k)$表示随机变量的k阶期望。

偏度

偏度是指随机变量的偏斜程度，偏度的计算公式如下：

$Skew(X)=E[\frac{(X-\mu)^3}{\sigma^3}]$

其中，$Skew(X)$表示随机变量的偏度，$\mu$表示随机变量的均值，$\sigma$表示随机变量的标准差。
偏度定义中包括正态分布（偏度=0），正偏态分布（右偏分布，偏度>0），负偏态分布（左偏分布，偏度<0）。

峰度

峰度是指随机变量的峰态程度，表征概率密度分布曲线在平均值处峰值高低的特征数。
峰度的计算公式如下：

$Kurt(X)=E[\frac{(X-\mu)^4}{\sigma^4}]$

其中，$Kurt(X)$表示随机变量的峰度，$\mu$表示随机变量的均值，$\sigma$表示随机变量的标准差。
峰度定义中包括正态分布（峰度=3），厚尾（峰度>3），薄尾（峰度<3）。
偏度和峰度是度量随机变量概率分布的不对称性和陡峭程度的指标，可以用来分析数据的形状和特征，区分数据的分布类型。

分位数和箱线图

分位数根据等分的形式可以分为四分位数、中位数、百分位数，四分位数的计算公式如下：

$Q_1=\frac{n+1}{4}$

$Q_2=\frac{n+1}{2}$

$Q_3=\frac{3(n+1)}{4}$

其中，$Q_1$表示第一四分位数，$Q_2$表示第二四分位数，$Q_3$表示第三四分位数，$n$表示数据的个数。
箱线图擅长于比较数据集中各组的分布情况，以一种简化的格式显示大量的信息。

$IQR=Q_3-Q_1$

$Q_1-1.5IQR\leq x\leq Q_3+1.5IQR$

其中，$IQR$表示四分位距，$Q_1$表示第一四分位数，$Q_3$表示第三四分位数，$x$表示数据，$n$表示数据的个数。

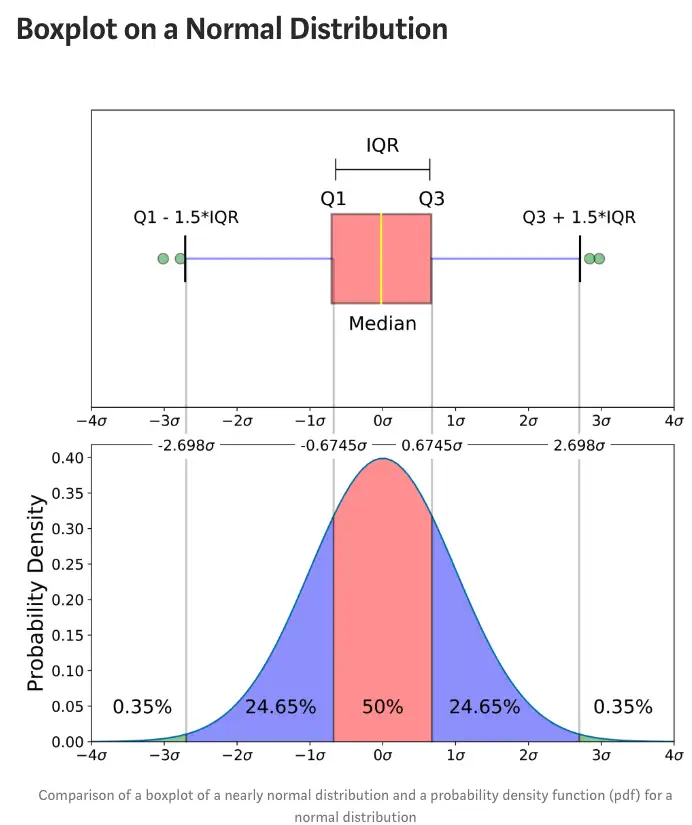
除了箱线图之外，还有核密度估计，小提琴图，qq图等描述数据分布的图形。

联合分布

联合分布是指两个或者多个随机变量的分布，联合分布的计算公式如下：

$F(x,y)=P(X\leq x,Y\leq y)$

其中，$F(x,y)$表示两个随机变量的联合分布，$P(X\leq x,Y\leq y)$表示两个随机变量的联合概率。
离散型随机变量的联合分布的计算公式如下：

$P(X=x_i,Y=y_j)=p_{ij}$

其中，$P(X=x_i,Y=y_j)$表示两个随机变量的联合概率，$p_{ij}$表示两个随机变量的联合概率。
连续型随机变量的联合分布的计算公式如下：

$F(x,y)=\int_{-\infty}^x\int_{-\infty}^yf(u,v)dudv$

其中，$f(x,y)$表示两个随机变量的联合概率密度函数，$F(x,y)$表示两个随机变量的联合分布。

边缘分布

边缘分布是指联合分布中的一个随机变量的分布，边缘分布的计算公式如下：

$F_X(x)=P(X\leq x)=P(X\leq x,Y<+\infty)=F(x,\infty)$

其中，$F_X(x)$表示一个随机变量的边缘分布，$P(X\leq x)$表示一个随机变量的概率，$P(X\leq x,Y<+\infty)$表示两个随机变量的联合概率，$F(x,\infty)$表示两个随机变量的联合分布。
离散型随机变量的边缘分布的计算公式如下：

$P(X=x_i)=\sum_{j=1}^np_{ij}$

其中，$P(X=x_i)$表示一个随机变量的边缘概率，$p_{ij}$表示两个随机变量的联合概率。
连续型随机变量的边缘分布的计算公式如下：

$f_X(x)=\int_{-\infty}^{+\infty}f(x,y)dy$

其中，$f_X(x)$表示一个随机变量的边缘概率密度函数，$f(x,y)$表示两个随机变量的联合概率密度函数。

条件分布

条件分布是指联合分布中的一个随机变量在另一个随机变量的条件下的分布，条件分布的计算公式如下：

$F_{X|Y}(x|y)=P(X\leq x|Y=y)=\frac{P(X\leq x,Y=y)}{P(Y=y)}$

其中，$F_{X|Y}(x|y)$表示一个随机变量在另一个随机变量的条件下的分布，$P(X\leq x|Y=y)$表示一个随机变量在另一个随机变量的条件下的概率，$P(X\leq x,Y=y)$表示两个随机变量的联合概率，$P(Y=y)$表示一个随机变量的边缘概率。

$f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}$

其中，$f_{X|Y}(x|y)$表示一个随机变量在另一个随机变量的条件下的概率密度函数，$f(x,y)$表示两个随机变量的联合概率密度函数，$f_Y(y)$表示一个随机变量的边缘概率密度函数。
对于连续性随机变量

$P(X\leq x,Y=y)=\int_{-\infty}^xf(u,y)du$

$P(Y=y)=\int_{-\infty}^{+\infty}f(u,y)du$

其中，$f(u,y)$表示两个随机变量的联合概率密度函数。

协方差矩阵

协方差矩阵是指多个随机变量之间的协方差，协方差矩阵的计算公式如下：

$Cov(X,Y)=E[(X-E(X))(Y-E(Y))]$

$\sum=\begin{bmatrix} Cov(X_1,X_1)&Cov(X_1,X_2)&\cdots&Cov(X_1,X_n)\\ Cov(X_2,X_1)&Cov(X_2,X_2)&\cdots&Cov(X_2,X_n)\\ \vdots&\vdots&\ddots&\vdots\\ Cov(X_n,X_1)&Cov(X_n,X_2)&\cdots&Cov(X_n,X_n) \end{bmatrix}$

其中，$Cov(X,Y)$表示多个随机变量之间的协方差，$E(X)$表示随机变量的期望，$E(Y)$表示随机变量的期望。

相关系数

相关系数是指多个随机变量之间的相关程度，相关系数的计算公式如下：

$\rho(X,Y)=\frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}$

其中，$\rho(X,Y)$表示多个随机变量之间的相关系数，$Cov(X,Y)$表示多个随机变量之间的协方差，$D(X)$表示随机变量的方差，$D(Y)$表示随机变量的方差。
相关系数的绝对值越大，相关程度越强，相关系数的绝对值越小，相关程度越弱。
相关系数接近于1，表示正相关，相关系数接近于-1，表示负相关，相关系数等于0，表示不相关。

多元正态分布

多元正态分布是指多个随机变量的正态分布，多元正态分布的计算公式如下：

$f(x)=\frac{1}{(2\pi)^{\frac{n}{2}}|\sum|^{\frac{1}{2}}}e^{-\frac{1}{2}(x-\mu)^T\sum^{-1}(x-\mu)}$

其中，$f(x)$表示多个随机变量的概率密度函数，$n$表示随机变量的个数，$\mu$表示随机变量的均值，$\sum$表示随机变量的协方差矩阵。

统计学

总体与样本

总体是指研究对象的全体，样本是指从总体中抽取的一部分，总体的计算公式如下：

$\mu=\frac{1}{N}\sum_{i=1}^Nx_i$

其中，$\mu$表示总体的均值，$N$表示总体的个数，$x_i$表示总体的取值。
样本的计算公式如下：

$\bar{x}=\frac{1}{n}\sum_{i=1}^nx_i$

其中，$\bar{x}$表示样本的均值，$n$表示样本的个数，$x_i$表示样本的取值。

样本比例

样本比例是指样本中某个特征的比例，样本比例的计算公式如下：

$p=\frac{m}{n}$

其中，$p$表示样本比例，$m$表示样本中某个特征的个数，$n$表示样本的个数。

总体方差

总体方差是指总体的离散程度，总体方差的计算公式如下：

$\sigma^2=\frac{1}{N}\sum_{i=1}^N(x_i-\mu)^2$

其中，$\sigma^2$表示总体方差，$N$表示总体的个数，$x_i$表示总体的取值，$\mu$表示总体的均值。

样本方差

样本方差是指样本的离散程度，样本方差的计算公式如下：

$s^2=\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})^2$

$E(s^2)=\sigma^2$

其中，$s^2$表示样本方差，$n$表示样本的个数，$x_i$表示样本的取值，$\bar{x}$表示样本的均值。

大数定律

大数定律是指样本均值的极限是总体均值，大数定律的计算公式如下：

$\lim_{n\to\infty}\bar{x}=\mu$

其中，$\lim_{n\to\infty}\bar{x}$表示样本均值的极限，$\mu$表示总体均值。

中心极限定理

中心极限定理是指样本均值的分布趋近于正态分布，中心极限定理的计算公式如下：

$\lim_{n\to\infty}P(\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\leq x)=\Phi(x)$

其中，$\lim_{n\to\infty}P(\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\leq x)$表示样本均值的分布，$\Phi(x)$表示标准正态分布。

点估计

点估计是指用样本统计量估计总体参数，点估计的计算公式如下：

$\hat{\theta}=g(x_1,x_2,\cdots,x_n)$

其中，$\hat{\theta}$表示总体参数的点估计，$g(x_1,x_2,\cdots,x_n)$表示样本统计量。

最大似然估计（MLE）

最大似然估计是指样本的概率密度函数最大的参数值，最大似然估计的计算公式如下：

$L(\theta)=\prod_{i=1}^nf(x_i;\theta)$

其中，$L(\theta)$表示样本的概率密度函数，$f(x_i;\theta)$表示样本的概率密度函数，$\theta$表示总体参数。

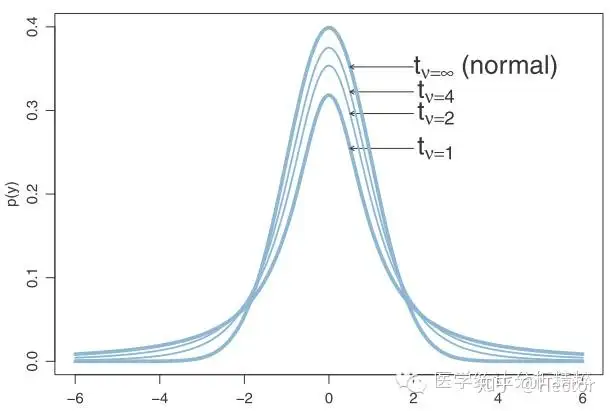
t分布

t分布的计算公式如下：

$T(n-1)=\frac{X}{\sqrt{Y/{n}}}$

其中，$T$表示样本均值的分布，$X$表示标准正态分布，$Y$表示卡方分布，$n$表示样本的个数。X~$N(0,1)$，Y~$\chi^2(n)$，X与Y相互独立。

置信区间

置信区间是指总体参数的估计区间，置信区间的计算公式如下：

$P(\theta_1\leq\theta\leq\theta_2)=1-\alpha$

其中，$P(\theta_1\leq\theta\leq\theta_2)$表示总体参数的估计区间，$\alpha$表示显著性水平。$1-\alpha$表示置信度。$\theta_1$为置信区间的下限，$\theta_2$为置信区间的上限。

假设检验

假设检验是指根据样本数据对总体参数提出假设，假设检验的计算公式如下：

$H_0:\theta=\theta_0$

$H_1:\theta\neq\theta_0$

其中，$H_0$表示原假设，$H_1$表示备择假设，$\theta$表示总体参数，$\theta_0$表示总体参数的假设值。

一类错误

一类错误是指拒绝原假设，但是原假设为真，一类错误的计算公式如下：

$P(\bar{x}\leq\theta_1)+P(\bar{x}\geq\theta_2)=\alpha$

其中，$P(\bar{x}\leq\theta_1)+P(\bar{x}\geq\theta_2)$表示一类错误，$\alpha$表示显著性水平。

二类错误

二类错误是指接受原假设，但是原假设为假，二类错误的计算公式如下：

$P(\theta_1\leq\bar{x}\leq\theta_2)=1-\beta$

其中，$P(\theta_1\leq\bar{x}\leq\theta_2)$表示二类错误，$\beta$表示二类错误的概率。

右尾检验

右尾检验是指备择假设为大于，右尾检验的计算公式如下：

$H_0:\theta\leq\theta_0$

$H_1:\theta>\theta_0$

其中，$H_0$表示原假设，$H_1$表示备择假设，$\theta$表示总体参数，$\theta_0$表示总体参数的假设值。

左尾检验

左尾检验是指备择假设为小于，左尾检验的计算公式如下：

$H_0:\theta\geq\theta_0$

$H_1:\theta<\theta_0$

其中，$H_0$表示原假设，$H_1$表示备择假设，$\theta$表示总体参数，$\theta_0$表示总体参数的假设值。

双尾检验

双尾检验是指备择假设为不等于，双尾检验的计算公式如下：

$H_0:\theta=\theta_0$

$H_1:\theta\neq\theta_0$

其中，$H_0$表示原假设，$H_1$表示备择假设，$\theta$表示总体参数，$\theta_0$表示总体参数的假设值。

P值(p-value)

P值是指在原假设为真的条件下，样本统计量的极端值出现的概率。如果P值小于显著性水平，说明小概率事件发生了，拒绝原假设，否则接受原假设。

拒接域

拒接域是显著性水平对应横轴上的区间。如果样本统计量落在拒接域内，拒绝原假设，否则接受原假设。

临界值

临界值是指置信区间和拒绝域的分界点。