机器学习

Arthur Samuel(1959)：机器学习是一门研究，如何使计算机可以不需要明确编程，而是通过经验自动改进的学科。

监督学习（Supervised Learning）

监督学习是指学习x到y或输入到输出的映射的算法，通过给学习算法示例，这些示例包括正确的标签，让模型学会根据输入，对输出给出合理准确的预测或猜测。

Input(x)	Output(y)	Application
email	spam/not spam	垃圾邮件过滤
audio	text transcript	语音识别
English	Chinese	机器翻译
ad, user info	click/not click	点击率预测
image,radar info	position of other cars	自动驾驶
image of phone	defects	视觉检测

回归

回归问题是指预测连续值输出的问题，如房价预测，股票价格预测等。

分类

分类问题是指预测离散值输出的问题，如垃圾邮件分类，疾病诊断等。

无监督学习（Unsupervised Learning）

无监督学习是一种不带标签的数据集学习，其目的是在数据中找到结构和模式。

聚类

无监督学习的一种特殊算法，通过将数据分配给不同的组或集群来寻找模式和结构，如Google news，社交网络分析，市场细分等。

异常检测

异常检测用于检测异常事件，如信用卡欺诈，工业部件故障等。

降维

降维是指将一个大数据集神奇地压缩成一个小得多的数据集，同时丢失尽可能少的信息，如可视化，数据压缩等。

一些术语

损失函数

损失函数是指衡量模型预测值与真实值之间差异的函数，如均方误差，交叉熵等。

平方损失函数

$J(w,b) = \frac{1}{2m}\sum_{i=1}^{m}(f_{w,b}(x^{(i)})-y^{(i)})^2$

梯度下降

梯度下降是一种优化算法，用于最小化损失函数，其思想是沿着损失函数的梯度方向，不断迭代更新参数，直到损失函数最小。

$w = w - \alpha\frac{\partial J(w,b)}{\partial w}$

$b = b - \alpha\frac{\partial J(w,b)}{\partial b}$

$w$是模型的参数，$b$是模型的偏置，$\alpha$是学习率，$\frac{\partial J(w,b)}{\partial w}$和$\frac{\partial J(w,b)}{\partial b}$分别是损失函数对w和b的偏导数。
更新过程

$tempw = w - \alpha\frac{\partial J(w,b)}{\partial w}$

$tempb = b - \alpha\frac{\partial J(w,b)}{\partial b}$

$w = tempw$

$b = tempb$

多类特征

多类特征是指数据集的输入有多个信息，例如人的信息有性别$x_1$，血型$x_2$，年龄$x_3$，身高$x_4$，体重$x_5$等，最后预测该人的颜值有多少分。

$f_{w,b}(x) = w_1x_1+w_2x_2+...+w_nx_n+b$

向量化

可以将w和x看成向量，将w和x的转置相乘，得到一个标量，即为预测值。

$w = \begin{bmatrix}w_1\\w_2\\...\\w_n\end{bmatrix}$

$x = \begin{bmatrix}x_1\\x_2\\...\\x_n\end{bmatrix}$

$f_{w,b}(x) = w^Tx+b$

向量化的速度比循环快很多。

特征缩放

特征缩放是指将数据集中的特征值缩放到一个范围内，例如将身高和体重的值缩放到0-1之间，这样可以加快梯度下降的收敛速度。

使用最大值缩放

$x_1 = \frac{x_1}{x_{1max}}$

$x_2 = \frac{x_2}{x_{2max}}$

$......$

$x_n = \frac{x_n}{x_{nmax}}$

使用均值缩放

$x_1 = \frac{x_1-\mu_{1}}{x_{1max}-x_{1min}}$

$x_2 = \frac{x_2-\mu_{2}}{x_{2max}-x_{2min}}$

$......$

$x_n = \frac{x_n-\mu_{n}}{x_{nmax}-x_{nmin}}$

使用Z-score缩放

$x_1 = \frac{x_1-\mu_{1}}{\sigma_{1}}$

$x_2 = \frac{x_2-\mu_{2}}{\sigma_{2}}$

$......$

$x_n = \frac{x_n-\mu_{n}}{\sigma_{n}}$

缩放范围

缩放范围不要太大，也不要太小。最大最好$-3≤x_{i}≤3$，最小最好$-1≤x_{i}≤1$。

检查梯度是否收敛

学习曲线

学习曲线是指损失函数随着迭代次数的变化曲线，可以通过学习曲线来判断梯度下降是否收敛。学习曲线的横坐标是迭代次数，纵坐标是损失函数的值。

自动检测

自动检测是指通过计算损失函数的值，来判断梯度下降是否收敛。当损失函数的值小于某个阈值$\epsilon（\epsilon = 10^{-3}）$时，认为梯度下降收敛。

超参数

超参数是指在训练模型之前需要设置的参数，如学习率，迭代次数等。不同于模型参数$w$、$b$，超参数需要人为设置，而模型参数是通过训练数据集得到的。

学习率

学习率是指梯度下降算法中的一个超参数，用于控制每次迭代更新参数的步长，学习率过大会导致损失函数震荡，学习率过小会导致收敛速度过慢。常用的学习率有1，0.1，0.01，0.001等。学习率的选择需要根据实际情况来确定（动态变化），可以通过学习曲线来判断学习率是否合适。

特征工程

特征工程是指通过对数据集的特征进行处理，来提高模型的性能，如特征缩放，特征选择，特征变换等。通过特征工程，可以提高模型的准确率，降低模型的过拟合程度，加快模型的训练速度等。

逻辑回归

虽然逻辑回归带有回归，但其实逻辑回归是一种分类算法（解决二分类问题），其输出是一个概率值，用于表示某个样本属于某个类别的概率，其输出值在0-1之间，当输出值大于0.5时，认为该样本属于该类别，当输出值小于0.5时，认为该样本不属于该类别。

Sigmoid函数（逻辑函数）

$g(z) = \frac{1}{1+e^{-z}}$

$z = w^Tx+b$

$0 ＜ g(z) ＜ 1$

sigmoid函数的输出在0-1之间，sigmoid函数图像如下：

有了sigmoid函数，我们可以得到更加复杂的决策边界，拟合更加复杂的数据集。

决策边界

决策边界是指将数据集分成两个部分的边界，决策边界可以是直线，也可以是曲线，如下图所示：

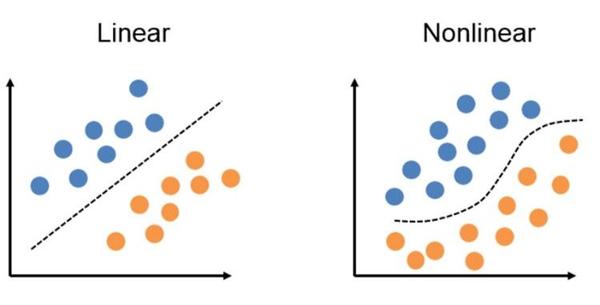
决策边界的表达式就是sigmoid函数的输入为0时，即$z=0$时，此时$w^Tx+b=0$，即$w_1x_1+w_2x_2+...+w_nx_n+b=0$。

逻辑回归的损失函数

逻辑回归如果使用平方损失函数，会导致损失函数是一个非凸函数，存在很多局部最优解，这样会导致梯度下降算法无法收敛到全局最优解，因此逻辑回归使用交叉熵损失函数。

交叉熵损失函数

$J(w,b) = -\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log(f_{w,b}(x^{(i)}))+(1-y^{(i)})log(1-f_{w,b}(x^{(i)}))]$

拟合

拟合是指通过训练数据集，得到一个模型，使得该模型能够对未知数据进行预测。

过拟合/high variance

过拟合是指模型在训练集上表现良好，但在测试集上表现不好，过拟合的原因是模型过于复杂，导致模型过于拟合训练集，从而导致模型泛化能力差。

解决过拟合

1. 增加训练数据集
2. 减少特征数量
3. 正则化（常用）

正则化

正则化是指在损失函数中加入正则项，使得模型的参数尽可能小，从而减少模型的复杂度，防止过拟合。

正则化的损失函数

L1正则化

$J(w,b) = -\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log(f_{w,b}(x^{(i)}))+(1-y^{(i)})log(1-f_{w,b}(x^{(i)}))]+\frac{\lambda}{2m}\sum_{j=1}^{n}|w_j|$

L2正则化

$J(w,b) = -\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log(f_{w,b}(x^{(i)}))+(1-y^{(i)})log(1-f_{w,b}(x^{(i)}))]+\frac{\lambda}{2m}\sum_{j=1}^{n}w_j^2$

$\lambda$为正则化参数，正则化只改变$w_{i}$，并没有改变$b$。$\lambda=0$，则没有进行正则化，$\lambda$越大，则所有的$w_i$接近于0，只剩下一个b，即$f_{w,b}(x) = w_1x_1+w_2x_2+...+w_nx_n+b≈b$。因此，需要选择一个合适的$\lambda$。

欠拟合/high bias

欠拟合是指模型在训练集上表现不好，也在测试集上表现不好，欠拟合的原因是模型过于简单，导致模型无法拟合训练集，从而导致模型泛化能力差。

神经网络

神经网络是一种模拟人脑神经元工作原理的算法，神经网络的每个神经元都有输入和输出，神经元的输入是其他神经元的输出，神经元的输出又作为其他神经元的输入，这样就形成了一个神经网络。

神经网络 = 输入层 + 多个隐藏层 + 输出层
多层神经网络也称作多层感知机（MLP）
下面是一个图像识别的神经网络

神经网络的计算公式

$a^{[l]}_{j} = g(w^{[l]}_{j}a^{[l-1]}+b^{[l]}_{j})$

$l$表示第$l$层，$j$表示第$j$个神经元，$a^{[l]}_{j}$表示第$l$层第$j$个神经元的输出,$w^{[l]}_{j}$表示第$l$层第$j$个神经元的权重，$a^{[l-1]}$表示第$l-1$层的输出，$b^{[l]}_{j}$表示第$l$层第$j$个神经元的偏置，$g$表示激活函数。

前向传播

前向传播是指从输入层到输出层的计算过程，前向传播的过程就是神经网络的计算过程，前一层的输出作为后一层的输入，直到输出层。

import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.losses import BinaryCrossentropy
# 创建神经网络的层
layer_1 = Dense(units=3, activation="sigmoid")
layer_2 = Dense(units=1, activation="sigmoid")
# 将层连接起来作为一个模型
model = Sequential([layer_1, layer_2])
# data
x = np.array([[200.0, 17.0],
[120.0, 5.0],
[425.0, 20.0],
[212.0, 18.0]])
y = np.array([1,0,0,1])
# 编译
model.compile(loss=BinaryCrossentropy(), optimizer="sgd", metrics=["accuracy"])
# 拟合
model.fit(x, y, epochs=1000)
# 预测
model.predict(np.array([[210.0, 27.0]]))

激活函数

激活函数是指神经元的输出函数，激活函数的作用是将神经元的输出映射到一个非线性的空间，从而使得神经网络可以拟合非线性的数据集。

ReLU函数

ReLU函数是指$g(z)=max(0,z)$，ReLU函数的图像如下：

激活函数的选择

1. 如果是二分类问题，输出层使用sigmoid函数
2. 如果是回归问题，输出层使用线性激活函数（不使用激活函数）
3. 如果是回归问题，输出不会出现负值（例如房价预测），输出层使用ReLU函数
   对于隐藏层，大多数人的选择都是ReLU函数，但是也有人选择其他激活函数，如tanh函数，sigmoid函数等。RuLU激活函数能够使模型快速学习，缩短训练时间。

多类问题

多类问题是指输出有多个类别的问题，如手写数字识别，猫狗识别等。

Softmax函数

Softmax函数是指$g(z)=\frac{e^{z}}{\sum_{i=1}^{n}e^{z_i}}$，其中$z_i$表示第$i$个神经元的输出/第$i$类的输出值，$n$表示神经元的个数。
Softmax激活函数与其他激活函数的区别是，其他激活函数的输出是一个标量，而Softmax激活函数的输出是一个向量，向量的每个元素表示一个类别的概率，所有类别的概率之和为1。

损失函数

多类问题的损失函数是交叉熵损失函数。

$J(w,b) = -\frac{1}{m}\sum_{i=1}^{m}\sum_{j=1}^{n}y^{(i)}_jlog(f_{w,b}(x^{(i)})_j)$

其中$y^{(i)}_j$表示第$i$个样本的第$j$个类别的标签，$f_{w,b}(x^{(i)})_j$表示第$i$个样本的第$j$个类别的预测值。

多标签输出（多个输出）

多标签输出是指输出有多个标签的问题，如人脸识别，人脸识别的输出有两个标签，一个是人脸的位置，一个是人脸的表情。

优化算法

优化算法是指用于优化损失函数的算法，常用的优化算法有梯度下降算法，随机梯度下降算法，批量梯度下降算法，Adam算法等。

Adam算法

Adam算法是一种自适应学习率的优化算法，Adam算法的学习率会随着模型的训练过程而动态变化。并且Adam算法不止一个学习率，对于每个参数，Adam算法都会维护一个属于该参数的学习率。
目前，Adam算法是最常用的优化算法。

层

卷积层

卷积层的神经元只观察前一层输入的一小块区域，这个区域称为感受野，卷积层的神经元只与感受野内的神经元相连。这样可以加快计算，需要的训练参数更少，从而减少过拟合。

改进模型

1. Get more training examples -> fixes high variance
2. Try smaller sets of features -> fixes high variance
3. Try getting additional features -> fixes high bias
4. Try adding polynomial features -> fixes high bias
5. Try decreasing $\lambda$ -> fixes high bias
6. Try increasing $\lambda$ -> fixes high variance
   将数据集划分为训练集，验证集，测试集，训练集用于训练模型，验证集用于选择模型，测试集用于测试模型。

增加数据

数据不够，如何增加数据？

数据增强（Data Augmentation）

数据增强是指通过对数据集进行一些变换，来增加数据集的大小，如水平翻转，垂直翻转，旋转，裁剪，缩放，平移，添加噪声，改变颜色等。
数据增强最有效的方式是裁剪+改变颜色。

数据合成（Data Synthesis）

数据合成是指通过一些算法，来生成数据，如GAN，VAE等。

迁移学习

迁移学习是指将一个已经训练好的模型，利用自己的数据集再次进行训练，从而加快模型的训练速度，提高模型的准确率。自己的模型要和网上下载的模型十分相似，比如都是分类任务，网上是分类猪牛，自己的任务是分类猫狗
机器学习社区中，有很多已经训练好的模型，这些模型的参数可以直接使用，而不需要重新训练。可以将这些训练好的模型下载下来，根据自己的数据集再次训练。
迁移学习为什么可行？因为神经网络的底层特征是可以共享的，底层特征是一些简单的特征，如边缘，纹理等，这些特征是可以共享的。底层特征由神经网络的浅层进行学习，这些特征对于不同的项目来说，几乎都是一样的。

所以，我们在别人的项目进行自己的实验时，我们可以修改深层的参数，调整浅层的参数。调整浅层参数有两种方法：

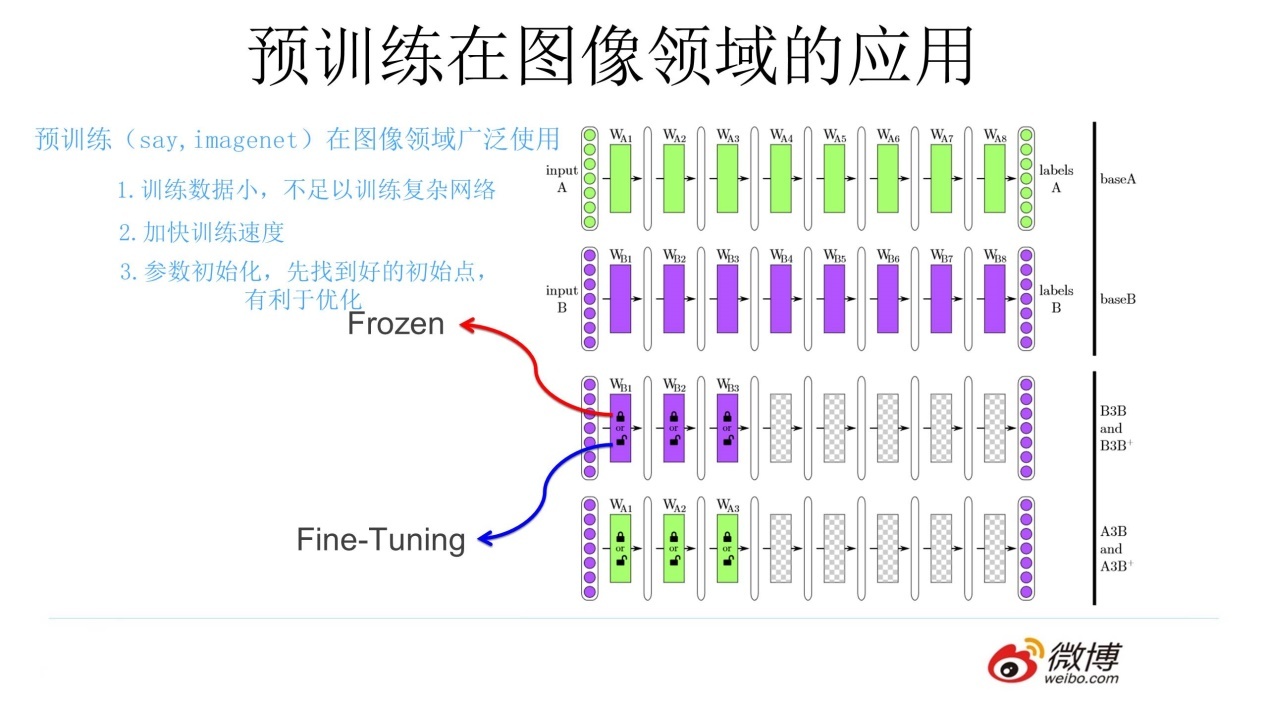
1. 冻结：保持浅层的参数不变，然后训练自己的模型
2. 微调：浅层参数随着自己任务的训练不断发生变化

数据集的误差指标

混淆矩阵（Confusion Matrix）

混淆矩阵是指将数据集的预测值和真实值进行比较，得到的一个矩阵，如下图所示：

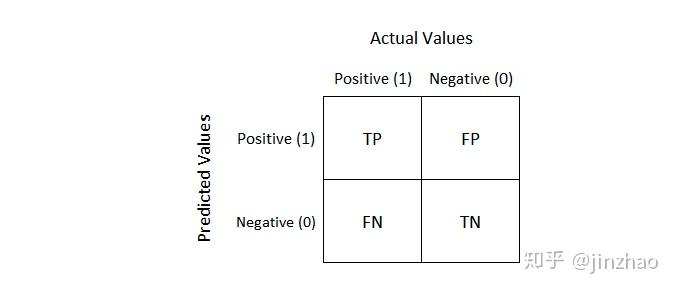
TP: True Positive，真正例，预测值为正，真实值为正
TN: True Negative，真负例，预测值为负，真实值为负
FP: False Positive，假正例，预测值为正，真实值为负
FN: False Negative，假负例，预测值为负，真实值为正

精确率（Precision）

精确率是指预测为正的样本中，真实为正的样本的比例，即$\frac{TP}{TP+FP}$。

召回率（Recall）

召回率是指真实为正的样本中，预测为正的样本的比例，即$\frac{TP}{TP+FN}$。

F1值（F1 Score）

在机器学习中，要确保精确率和召回率都很高，但是精确率和召回率是一对矛盾的指标，精确率高，召回率就会低，召回率高，精确率就会低。因此，需要一个指标来同时衡量精确率和召回率，这个指标就是F1值。
F1值是指精确率和召回率的调和平均数，即F1_$score = \frac{2}{\frac{1}{P}+\frac{1}{R}} = \frac{2PR}{P+R}$。

决策树（Decision Tree）

决策树是一种分类算法，其思想是通过一系列的问题，来对数据集进行分类，如下图所示：

选择结点

选择结点的一个原则是，选择的结点应该使得数据集的纯度提高，纯度是指数据集中同一类别的样本的比例，纯度越高，数据集的纯度越高。（其实就是经过了该结点之后，数据能够被很好的区分）
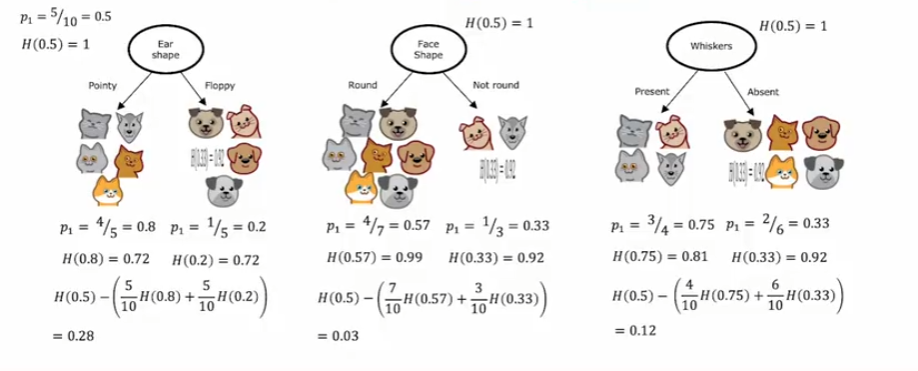
可以使用熵（Entropy）作为纯度的测量指标，熵越大，数据集的纯度越低，熵越小，数据集的纯度越高。下面是针对猫狗分类的数据集，经过结点之后，每种情况的熵的结果:

上图熵的公式为:

$H(p_1) = -p_1log p_1-(1-p_1)log (1-p_1)$

为了得到熵的图像，定义$0log0=0$

信息增益（Information Gain）

信息增益是指经过结点之后，数据集的熵的减少量，信息增益越大，数据集的纯度提高的越多，信息增益越小，数据集的纯度提高的越少。
信息增益的公式为:

$IG = H(p_1) - \sum_{i=1}^{n}\frac{N_i}{N}H(p_{i1})$

其中$H(p_1)$表示经过结点之前的熵，$\sum_{i=1}^{n}\frac{N_i}{N}H(p_{i1})$表示经过结点之后的熵，$N_i$表示经过结点之后，第$i$种情况的样本数量，$N$表示经过结点之后的样本数量。

独热编码（One-hot Encoding）

独热编码主要是采用N位状态寄存器来对N个状态进行编码，每个状态都有它独立的寄存器位，并且在任意时候，其中只有一位有效。如下图所示：

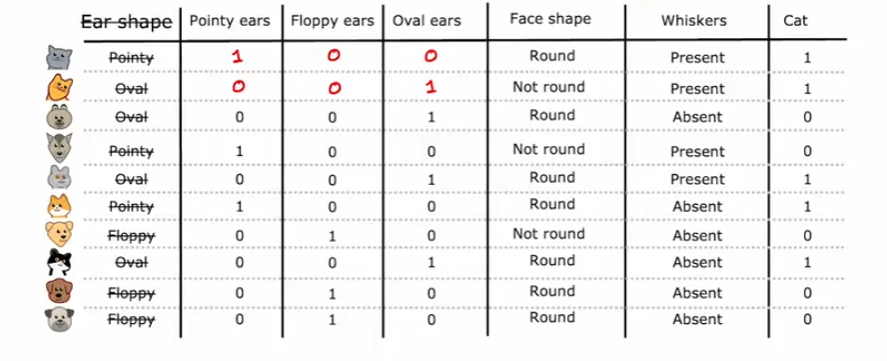
将Ear shape的特征去除，转化为Pointy ears、Floppy ears和Oval ears三个特征，每个特征只有两种情况，使用独热编码记录下来进行表示。

多决策树

多决策树是指将多个决策树组合起来，形成一个更加强大的模型，这样可以增加模型的准确率与鲁棒性，使模型更加健壮。

随机森林（Random Forest）

随机森林算法是一种强大的树集成算法，比使用单个决策树工作得更好，随机森林算法的思想是，当每个样本有M个属性时，在决策树的每个节点需要分裂时，随机从这M个属性中选取出m个属性，满足条件$m << M$（$m = \sqrt{M}$）。然后从这m个属性中采用某种策略（比如说信息增益）来选择1个属性作为该节点的分裂属性，构建多个决策树，然后将这些决策树组合起来，形成一个更加强大的模型。

XGBoost

XGBoost算法在机器学习竞赛和商业应用中被广泛使用，XGBoost算法是一种梯度提升算法，其思想是通过对薄弱的学习器进行改进，来构建一个更加强大的模型。
Classification

from xgboost import XGBClassifier
model = XGBClassifier()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)

Regression

from xgboost import XGBRegressor
model = XGBRegressor()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)

Decision Trees vs Neural Networks

Decision Trees and Tree ensembles

1. Works well on tabular (structured) data
2. Not recommended for unstructured data (images, audio, text)
3. Fast to train
4. Small decision trees may be human interpretable

Neural Networks

1. Works well on all types of data, including tabular(structured) and unstructured data
2. May be slower than a decision tree
3. Works with transfer learning
4. When building a system of multiple models working together, it might be easier to string together multiple neural networks

机器学习的迭代周期

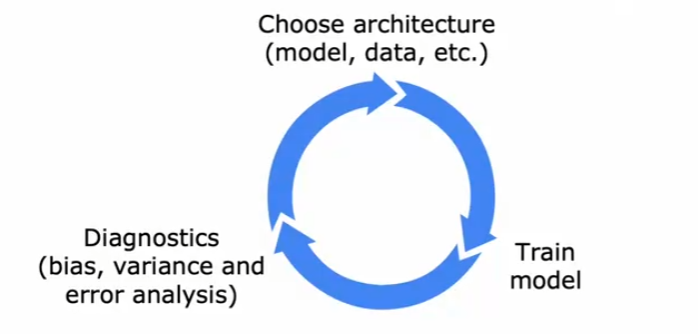
机器学习的完整周期

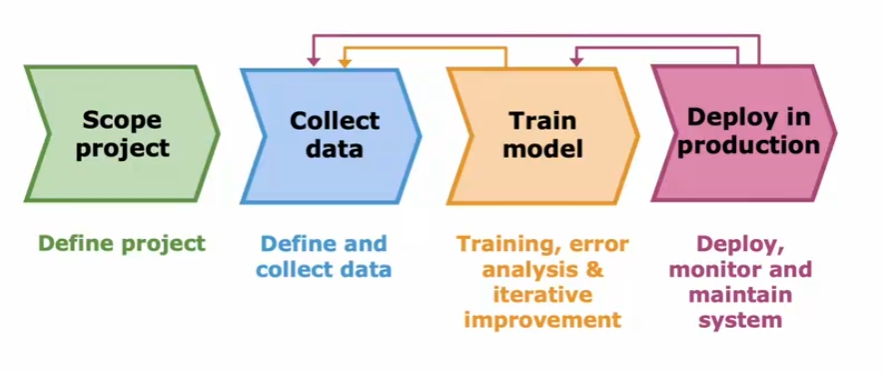
聚类算法（Clustering）

聚类算法是一种无监督学习算法，可以自动查找相互关联或相似的数据点，并将其分组为集群。聚类算法在新闻文章分组、市场细分、DNA分析、天文学和太空探索等领域都有广泛引用。

K-Means算法

K-Means算法是一种聚类算法，其思想是将数据集分成K个簇，每个簇都有一个中心点，每个数据点都属于距离它最近的中心点所在的簇。
初始化时中心点的选择最好尝试多次，否则会导致K-Means算法陷入局部最优解。建议使用多个随机初始化来最小化失真代价函数，并选择给出最低成本的集群集。随机初始化中心点的个数一般为50-1000。
选择k（簇数）的方法：Elbow Method（肘部法则）

异常检测

异常检测是一种无监督学习算法，用于检测异常事件，如信用卡欺诈，工业部件故障等。异常检测算法的目的是找到数据集中的异常事件，异常事件是指与大多数事件不同的事件，异常事件也称为离群点。
异常检测算法，可以帮助我们探测或发出危险信号。通过对未标记数据的分析，设置正常事件，可以学会探测不寻常的事件。异常检测在欺诈检测、制造业等领域有广泛应用。

推荐系统

推荐系统是一种无监督学习算法，用于预测用户可能感兴趣的物品，如电影，音乐，书籍等。推荐系统的应用场景有电影推荐，音乐推荐，商品推荐等。

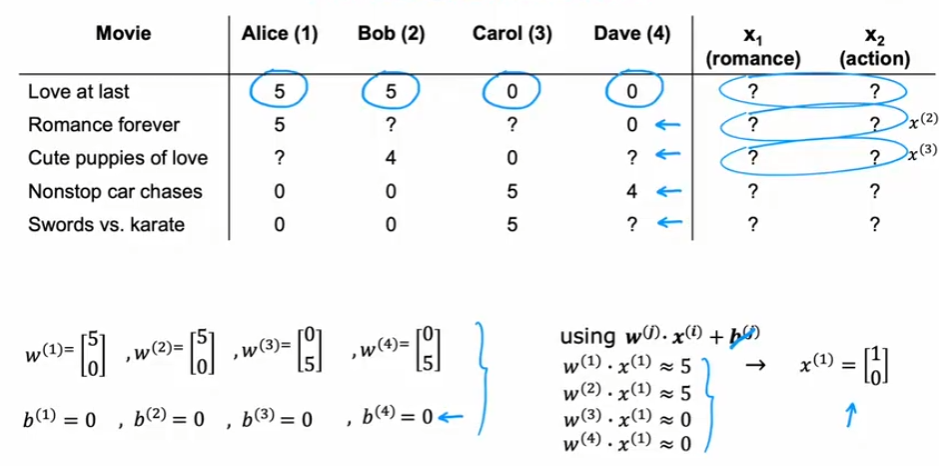
使用每项特征

将每项的特征作为输入，将用户对该项的评分作为输出，使用监督学习算法，如线性回归，逻辑回归，神经网络等。

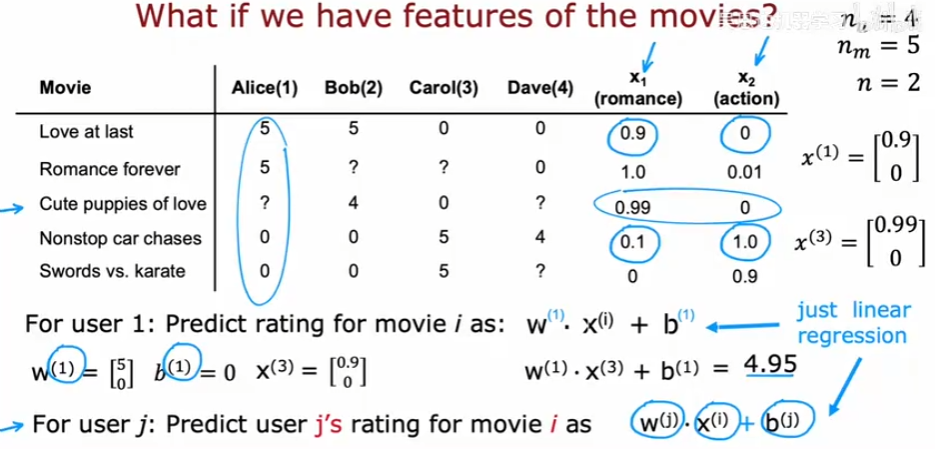
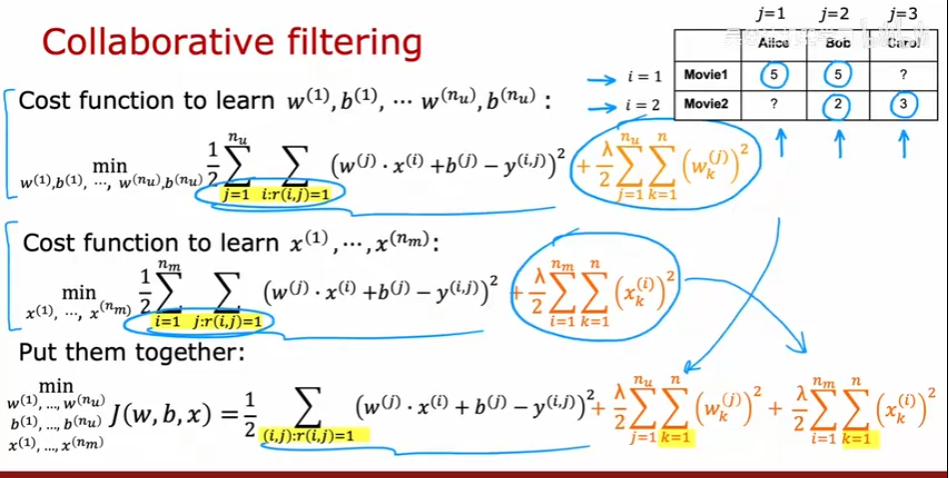
协同过滤算法

如果我们没有每项的特征，只有用户对每项的评分，如何预测用户对某项的评分？可以使用协同过滤算法，协同过滤，从字面上理解，包括协同和过滤两个操作。所谓协同就是利用群体的行为来做决策(推荐)，生物上有协同进化的说法，通过协同的作用，让群体逐步进化到更佳的状态。对于推荐系统来说，通过用户的持续协同作用，最终给用户的推荐会越来越准。而过滤，就是从可行的决策(推荐)方案(标的物)中将用户喜欢的方案(标的物)找(过滤)出来。具体来说，协同过滤的思路是通过群体的行为来找到某种相似性(用户之间的相似性或者标的物之间的相似性)，通过该相似性来为用户做决策和推荐。
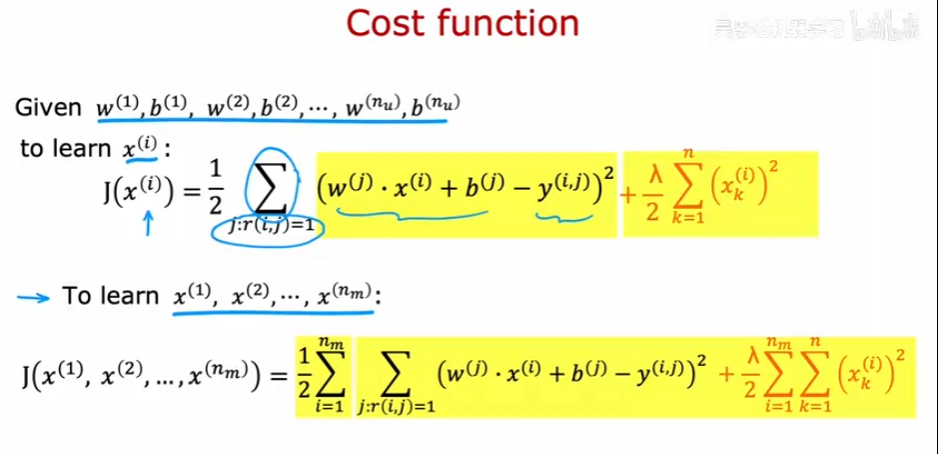
参数和特征进行随机初始化，之后使用损失函数进行梯度下降

$w^{(j)}_{i} = w^{(j)}_{i} - \alpha\frac{\partial J(w,b,x)}{\partial w^{(j)}_{i}}$

$b^{(j)} = b^{(j)} - \alpha\frac{\partial J(w,b,x)}{\partial b^{(j)}}$

$x^{(i)}_{j} = x^{(i)}_{j} - \alpha\frac{\partial J(w,b,x)}{\partial x^{(i)}_{j}}$

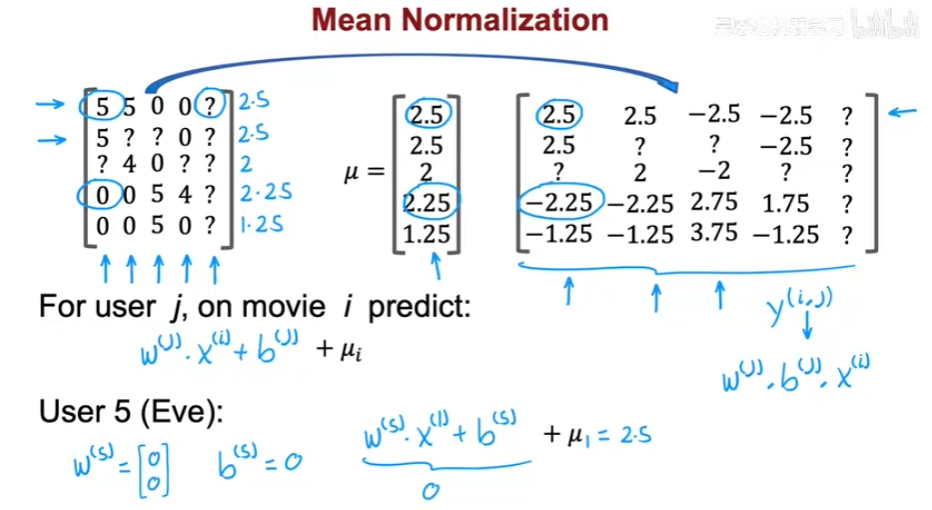
均值归一化

均值归一化用于处理空白的数据，通过计算已知数据的均值，之后根据式子来预测空白的数据。

基于内容的推荐系统

所谓基于内容的推荐算法(Content-Based Recommendations)是基于标的物相关信息、用户相关信息及用户对标的物的操作行为来构建推荐算法模型，为用户提供推荐服务。这里的标的物相关信息可以是对标的物文字描述的metadata信息、标签、用户评论、人工标注的信息等。用户相关信息是指人口统计学信息(如年龄、性别、偏好、地域、收入等等)。用户对标的物的操作行为可以是评论、收藏、点赞、观看、浏览、点击、加购物车、购买等。基于内容的推荐算法一般只依赖于用户自身的行为为用户提供推荐，不涉及到其他用户的行为。

怎么找到相似的物品呢？可以使用检索和排名两个步骤，检索是指根据用户的历史行为，找到与用户历史行为相似的物品，形成一个候选列表。排名是指根据候选列表，对物品进行排序，将排名靠前的物品推荐给用户。

强化学习

强化学习是一种机器学习算法，其目的是通过与环境的交互，来学习如何做出最优的决策。强化学习的应用场景有机器人，自动驾驶，游戏等。

奖励机制

强化学习的核心思想是奖励机制，奖励机制是指当智能体做出正确的决策时，给予奖励，当智能体做出错误的决策时，给予惩罚。智能体的目标是最大化奖励。

回报Return

回报是指智能体在某个状态下，做出某个动作后，所获得的奖励，回报的公式为:

$R_t = r_{t+1} + r_{t+2} + r_{t+3} + ... + r_{T}$

为了能够节约时间，我们可以使用折扣回报，折扣回报的公式为:

$R_t = r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + ... + \gamma^{T-t-1}r_{T}$

其中$\gamma$为折扣因子，$\gamma$越大，越重视未来的奖励，$\gamma$越小，越重视当前的奖励。

策略Policy

策略是指智能体在某个状态下，做出某个动作的概率，策略的公式为:

$\pi(a|s) = P[A_t=a|S_t=s]$

其中$\pi(a|s)$表示在状态$s$下，做出动作$a$的概率，$P[A_t=a|S_t=s]$表示在状态$s$下，做出动作$a$的概率。

Markov Decision Process（MDP）

Markov Decision Process（MDP）是指智能体在某个状态下，做出某个动作后，会转移到另一个状态，这个过程是一个马尔可夫过程。这个过程不依赖于之前的状态，只依赖于当前的状态。

状态动作值函数（Q函数）

状态动作值函数（Q函数）是指在某个状态下，做出某个动作后，所获得的回报，状态动作值函数的公式为:

$Q(s,a)/Q^{*}(s,a) = E[R_t|S_t=s,A_t=a]$

其中$Q(s,a)/Q^{*}(s,a)$表示在状态$s$下，做出动作$a$所获得的回报，$E[R_t|S_t=s,A_t=a]$表示在状态$s$下，做出动作$a$所获得的回报。

Bellman方程

Bellman方程是指状态动作值函数（Q函数）的递归表达式，Bellman方程的公式为:

$Q(s,a) = R(s) + \gamma max_{a'}Q(s',a')$

其中$Q(s,a)$表示在状态$s$下，做出动作$a$所获得的回报，$R(s)$表示在状态$s$下，所获得的奖励(及时奖励)，$\gamma$表示折扣因子，$max_{a'}Q(s',a')$表示在状态$s'$下，做出动作$a'$所获得的回报。$s'$经过一步操作后，可以达到$s$。

随机马尔可夫决策过程

$Q(s,a) = R(s) + \gamma E[max_{a'}Q(s',a')]$

$s'$经过多步操作后，可以达到$s$。

连续状态空间

对于连续状态空间，我们可以记录下每个状态的特征，比如位置、角度、速度、角速度等，然后再使用奖励机制，进行决策。结合深度学习，使用神经网络来拟合状态动作值函数（Q函数）。

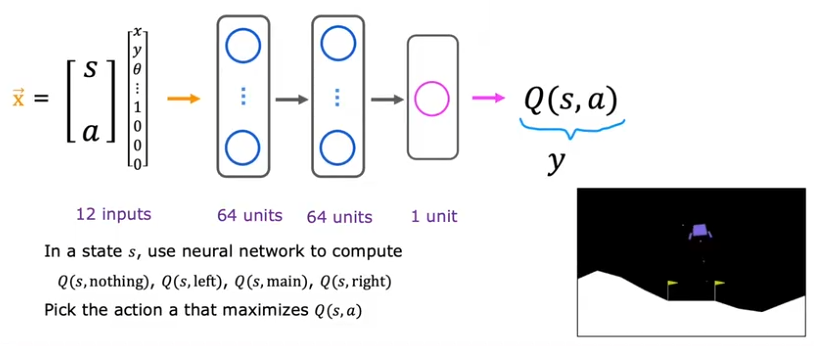
改进的神经网络架构

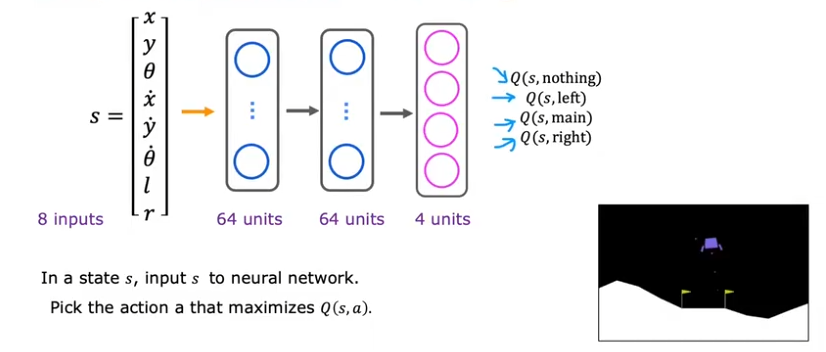
贪婪策略

$\epsilon$-贪婪策略是指在某个状态下，以$1-\epsilon$的概率选择最优的动作，以$\epsilon$的概率选择随机的动作，$\epsilon$越大，越倾向于选择随机的动作，$\epsilon$越小，越倾向于选择最优的动作。

迷你批量

迷你批量是指每次训练时，不是使用所有的数据，而是使用一部分数据，这样可以加快训练速度，减少内存的使用。当数据集非常大时，Mini-batch的使用比Adam的使用更为常见。

软更新

传统的更新

$w = w_{new}$

软更新

$w = 0.01w_{new} + 0.99w$

软更新可以使强化学习算法更加可靠的收敛，防止Q函数发生突变。